1、2、3、4、…が表のように並んでいます。たとえば、1行3列目の数は5で、3行1列目の数は9です。このとき、次の問いに答えなさい。

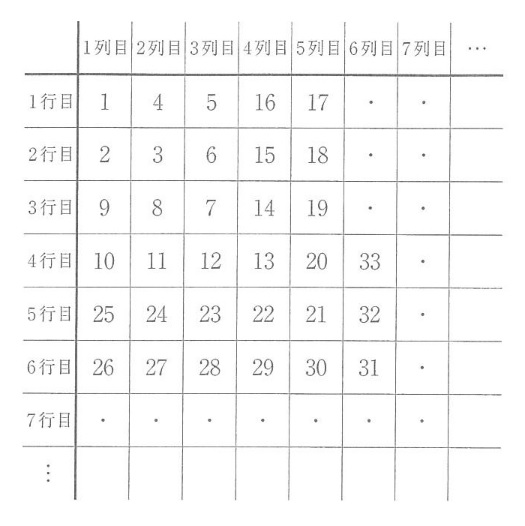
(1)1行8列目の数は何ですか。
(2)9行1列目の数は何ですか。
(3)450は何行何列目の数ですか。
(4)2行目の1列目から20列目までの20個の数のうち、3の倍数は何個ですか。

【解説と解答】
(1)偶数の平方数が1行目、奇数の平方数が1列目にきます｡1行6列目が6×6＝36、1行8列目は8×8＝64です。
(答え) 64
(2)1行1列目1、3行1列目3×3＝9、5行1列目5×5＝25、
7行1列目7×7＝49、9行1列目9×9＝81。
(答え)81
(3)450で一番近い平方数は21×21＝441でこれは奇数の平方数だから21行1列目。次の442は22行1列目になるから、450－441＝9から、450は22行9列目。
(答え)22行9列目
(4)１行目と2行目を並べてみると、
1、4、5、16、17、36、37、64、65、100、101、144、145
2、3、6、15、18、35、38、63、66、　99、102、143、146
となるので、2列目から３の倍数が4個続いて、2個途切れ、また4個続いて、2個途切れる、という規則になります。
これは３の約数を含まない偶数（４や16）はその１つ前が３の倍数になりますから右どなりも３の倍数になり、３の約数を含む平方数（36や144）はそれ自身が３の倍数になるので、１つ前も２つ後も３の倍数になりません。最初の１つを除き、そのあとの6個で4個が３の倍数になるので、
20－１＝19
19÷６＝３…１から４×３＋１＝13個が３の倍数です。
（答え）13個

2022年の出題です。

パーツＡを３個とパーツＢを４個組み合わせて製品Ｐが１個できます。ある工場では、製品Ｐを毎日20個ずつ作ります。この工場には、もともとＡ、Ｂのどちらのパーツもいくつかありますが、毎朝パーツＡが20個、パーツＢが30個届きます。両方のパーツが届いてから製品Ｐを作り始めるとき、次の問いに答えなさい。

（１）Ａ、Ｂのどちらのパーツも不足することなく製品Ｐを７日間作るとき、パーツＡ、パーツＢはそれぞれ何個使いますか。
（2）作り始めてから数日後に製品Ｐを作り終えたところ、パーツＡもパーツＢもちょうどなくなりました。このとき、もともと工場にあったパーツＡとパーツＢの個数の比をもっとも簡単な整数の比で答えなさい。
（3）作り始めてから30日目に製品Ｐを作り終えたところ、どちらか一方のパーツだけがちょうどなくなりました。もともと工場にあったパーツＡとパーツＢの個数の比が５：６であったとき、どちらのパーツが何個残りましたか。

【解説と解答】
（１）
P20個にはAが３×20＝60個　Bが４×20＝80個必要です。
7日間ですから、Aは60×７＝420個　Bは80×7＝560個
（答え）A　420個　B　560個
（２）1日にAは60個使い、Bは80個使います。
作った日数をX日、最初にあった個数をそれぞれA、Bとすると
A＋20×X＝60×X
B＋30×X＝80×X
ですからAは40×X、Bは50×XになるのでA：B＝４：５
（答え）４：５
（３）30日でAは60×30＝1800個、Bは80×30＝2400個です。
また届いたAは20×30＝600個　Bは30×30＝900個です。
Aがなくなっていれば、最初にあったAが1200個になり、Bは1440個になりますが、2400－900＝1540個でBが足りません。
Bがなくなっていれば、最初にあったBが1500個になり、最初にあったAは1250個になり、Aが50個残ります。

（答え）Aが50個残った。

2022年のm出題です。

図のように、たて2列、横6列に並んだ合計12席の座席があります。その中から前後左右となり合わないように5席の座席を選ぶとき、選び方は何通りありますか。

【解説と解答】
横1列に６つ席があり、両隣に座らないとなると最大で3席になり、
〇●〇●〇●という形（A）と〇●●〇●〇（B）の２つが考えられます。
（〇が座る席、●が空ける席）
この後ろの列に2席をとるには
Aの場合
〇●〇●〇●　〇●〇●〇●　〇●〇●〇●
●〇●〇●●　●●●〇●〇　●〇●●●○
の３通りがあり、前列と後列をひっくり返すともう3通り、さらに前列は一番左が●で始まる場合があるので、合計12通りあります。
Bの場合は
〇●●〇●〇　〇●●〇●〇　　〇●〇●●〇　〇●〇●●〇
●○●●○●　●●○●○●　　●○●●○●　●○●○●●

これが前後の交換で8通りですが、前列左から白にすると白が２つつながるので条件に反します。
したがって合計12＋8＝20通り
（答え）20通り

2022年の問題です。

２から2022までの整数のうち、０、２、４、６、８だけを使ってできるものを、次のように小さい順に並べていきます。

２、４、６、８、20、22、24、…、2022

このとき、次の問いに答えなさい。

（１）小さいほうから数えて20番目の数は何ですか。
（２）全部で何個の数が並んでいますか。
（３）全部の数の和はいくつになりますか。

【解説と解答】
（１）１の位は２、４、６、８、０の繰り返しで進んでいきます。
したがって20番目は20÷５＝4回で、
20が5番目、40が10番目…ですから、80が20番目です。
（答え）80
（２）2022が最後ですから4桁は
2000、2002、2004、2006、2008、2020、2022の7個です。
3桁の最後の数は888になるので、
ここまで
1桁4個、2桁20～88まで ５×４＝20個
3桁は200から始まるので202、204、206、208と続くから25個
25×4＝100個ですから、合計4＋20＋100＋７＝131個
（答え）131個
（３）131個あるので、
１の位は131÷５＝26…1で最後が２ですから
２＋４＋6＋８＋０＝20から20×26＋２＝522
10の位は131－４＝127個あり、127÷５＝25…2で最後のあまりの２は2020と2022の10の位になるから、
（20×25＋２＋２）×10＝5040
100の位は131－24＝107個あり、107÷（５×5）＝４…７
20×25×100＝50000
1000の位は2000×７＝14000
522＋5040＋50000＋14000＝69562
（答え）69562

太郎くんは毎日午後6時に駅でお父さんと会い，車で家に帰ります。ある日，太郎くんは午後5時32分に駅に着いたので，家に向かって毎時5kmの速さで歩き始めました。お父さんは太郎くんを迎えに行くために，午後6時ちょうどに駅に着くように午後5時47分に車で家を出ましたが，途中で太郎くんと出会ったので，太郎くんを車に乗せてすぐに家に向かい，午後6時5分に家に着きました。このとき，次の問いに答えなさい。ただし，車の速さはいつも一定です。

（1）太郎くんとお父さんが出会ったのは午後何時何分ですか。

（2）車の速さは毎時何kmですか。

（3）駅から家までの道のりは何kmですか。

【解説と解答】
（１）お父さんは5時47分に家を出て6時5分に帰っているので、18分動いていますから、片道は9分。つまり5時56分に太郎君と出会っています。
（答え）午後5時56分
（２）太郎君は5時32分に駅を出発しているので、24分歩いていますから
5×24/60＝2ｋｍ移動しました。本来、6時に着くのに午後5時56分に出会っていることから、２ｋｍを4分で移動することになるので、２÷4/60＝30ｋｍ
（答え）30ｋｍ
（３）いつもは13分かかっていますから、30×13/60＝6.5ｋｍ
（答え）6.5ｋｍ

2011年の出題です。

はじめにA，B，Cの3人はカードを何枚か持っています。まず，Aの持っているカードの1/7をCに渡し，Bの持っているカードの1/3をCに渡します。次に，Aの残りのカードの1/6をBに渡すとAとBが持っているカードの枚数の比は5：4になり，Cが持っている枚数は，はじめにCが持っていた枚数の6倍になりました。このとき，次の問いに答えなさい。
（1）はじめに持っていたAとBのカードの枚数の比を，もっとも簡単な整数の比で答えなさい。
（2）はじめに持っていたAとCのカードの枚数の比を，もっとも簡単な整数の比で答えなさい。
（3）最後にBとCのカードの枚数の和が100枚以上であるとき，Aが持っているカードの枚数として考えられるもっとも少ない枚数を求めなさい。

【解説と解答】
（１）最後のAとBの枚数を 【5】と【4】とすると
Aはその1/6をBにあげたので、その前は【5】÷５×６＝【6】になりますからBに渡ったのは【1】。さらにAは1/7をCに渡しているので、【6】÷6×７＝【7】がAの最初です。
一方BはAから【1】もらったので【3】。それがCに1/3を渡した残りですから、Bは
【3】÷２×３＝【4.5】したがって最初のA：B＝【7】：【4.5】＝14：９
（答え）14：9
（２）CはAから【1】もらい、Bから【1.5】もらったので【2.5】もらいましたが、それで最初の6倍になったので、【2.5】が最初の5倍になるから【2.5】÷5＝【0.5】
最初のA：C＝【7】：【0.5】＝14：1です。
（答え）14：１
（３）
整理すると

A 14 12 12 10
B 9 9 ６ 8
C 1 3 ６ 6
となります。
カードの枚数は整数になるので、（14）が100以上の整数になるのは112枚です。
したがって112÷14＝8枚からAの持っている枚数の最小は80枚
（答え）80枚