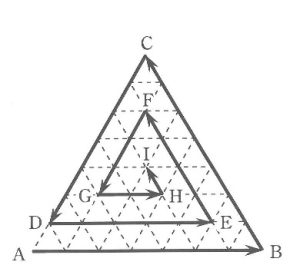
右の図のように、1辺の長さが7cmの正三角形ABCの各辺を７等分する点を結んでできた点線の上を、Aから出発して、B、C、……と経由して、 Iまで進むルートを考えます。
動く2つの点Xと点Yは、このルート上を、同時に点Aを出発して、点Xは毎秒3.5 cm の速さで、点Yは毎秒1.5 cm の速さで、点Iまで移動します。

このとき、次の問いに答えなさい。

(1)点Xが点Iに到達するまでに、点Yが移動した距離は何cmですか。

(2)点Xが点Cに到達したとき、三角形XIYの面積は三角形ABCの面積の何倍ですか。

(3)三角形AXYが正三角形となるのは何回ありますか。また、それはXとYがAを出発してから、何秒後ですか。

【解説と解答】
（１）ABが７cm、BCが7cm、CDが６cm、DEが５cm、EFが４cmとBCから1cmずつ短くなって最後IHが1cmです。（１＋７）×７÷２＋７＝35cmですから
35÷3.5＝10秒　したがってYが移動した距離は1.5×10＝15cm

（答え）15cm

（２）点XがCに到達したとき、14cm移動していますから、14÷3.5＝4秒後
Yは1.5×４＝6cmですから、Bの手前1cmのところにいます。右図でXI：IP＝４：３です。
またPY：YB＝2.5：１＝５：２

三角形XIYは三角形ABCの××＝

（答え）倍

（３）（２）から、XがCのとき、YがB手前1cmですから、１÷（3.5＋1.5）＝0.2秒後にXYはBCに平行になるので、これが1回目で4.2秒後。
三角形AXYが正三角形になるためには、XとYがAB上もしくはAC上にいなければならないので、これ以外にはありません。
（答え）１回、4.2秒後

【動画解説】