次の表のように、数を5で割った余りによって、5種類のグループに分類します。 この表を参考にして、次の問いに答えなさい。

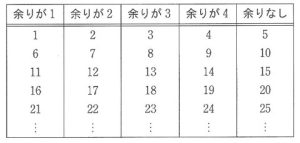
(1)「余りが1」のグループから2つの数を取り出し、その2つの数の積を作ります。 この積はどのグループの数になりますか。下の選択肢ア～オの中から1つ選び、 記号で答えなさい。
【選択肢】
ア 「余りが1」のグループ イ 「余りが2」のグループ
ウ 「余りが3」のグループ エ 「余りが4」のグループ
オ 「余りなし」のグループ
(2)下の選択肢ア～ケの中で、2つの数の積が「余りが1」のグループになる組み合わせとして適するものをすべて選び、記号で答えなさい。
【選択肢】
ア 「余りが1」のグループと「余りが2」のグループから1つずつの数
イ 「余りが1」のグループと「余りが3」のグループから1つずつの数
ウ 「余りが1」のグループと「余りが4」のグループから1つずつの数
エ 「余りが2」のグループから2つの数
オ 「余りが2」のグループと「余りが3」のグループから1つずつの数
カ 「余りが2」のグループと「余りが4」のグループから1つずつの数
キ 「余りが3」のグループから2つの数
ク 「余りが3」のグループと「余りが4」のグループから1つずつの数
ケ 「余りが4」のグループから2つの数
(3)3つの袋A、B、Cがあります。それぞれの袋には25個の球が入っており、それらの球には1から25までの数が1つずつかかれています。
袋A、B、Cから球を1個ずつ取り出すとき、取り出した3つの球にかかれている数の積が、5で割ると1余る数になる取り出し方は何通りありますか。

【解説と解答】
(1) ６×11＝66、11×21＝231、のように１の位が必ず１か６になるので、「余りが１」のグループになります。
(答え)ア
(2)１の位が１か６になればいいので、「余りが２」のグループと「余りが３」のグループから１つずつ選ぶ場合と、「余りが４」のグループから２つ選ぶ場合の２つが必ず１のグループになります。

(答え)オ、ケ
(3) (1) (2)から2数の場合は以下のア～ウの場合、１の位が「余りが１」のグループになります。
「余りが１」のグループから2数…ア
「余りが２」のグループと「余りが３」のグループから１数ずつ…イ
「余りが４」のグループから2数…ウ
があります。したがって３つの積の場合は
ア、イ、ウにそれぞれ「余りが１」のグループの数をかけることになります。
「余りが１」のグループから「余りなし」の数までは１～25の間にそれぞれ５個あります。
A、B、Cの積で考えると
①全部の数が「余りが１」のグループ
②「余りが２」のグループと「余りが３」のグループと「余りが１」のグループ
③「余りが４」のグループ２つと「余りが１」のグループ１つ
さらに、
④「余りが３」のグループ２つと「余りが４」のグループ１つ
⑤「余りが２」のグループ２つと「余りが４」のグループ１つ
が「余りが１」のグループになります。
①は５×５×５＝125通り。
②は5×5×5×３×２×１＝750通り　
③、④、⑤は5×5×5×３＝375通り

125＋750＋375×３＝2000
(答え)2000通り