2025年度第1回の算数です。

続きを読む →

2025年10月より、鴎友学園進学館WEB会員をスタートさせました。

鴎友学園進学館では鴎友学園受験のためのさまざまな情報や教材を掲載していますが、この中から会員専用のコンテンツを用意し、慶應3校の受験準備にお役立ていただくものです。

近年、学校別対策は重要視されていますが、各校まで細かく学校別特訓が設置されているところは少なく、また特に６年生の２学期は通塾の負担が大きくなるので、オンラインでの学校別対策が必要になってきています。

そこで鴎友学園進学館ではWEB会員制度を立ち上げることとなりました。フリーダムオンラインのWEBワークスに加えて鴎友学園合格に必要な対策を網羅するコンテンツをオンラインでお届けします。

そのひとつが国語過去問の添削指導です。過去の過去問をWEBページに掲示しますので、それをご自宅で印刷、問題を時間内に解いて専用システムよりアップロードいただけますと、専任講師が採点、添削をしてお返しするシステムになっています。その他、過去問の詳しい解説も掲載していきます。中心は算数と理科になりますが、それ以外にもご相談いただければ、より細かいオンラインの個別指導も受講することが可能です。（別費用）
WEB会員は、年会費制度となります。コンテンツは過去のものを含めてすべてご覧いただけますが、その利用期間が翌年の2月15日までとなります。年会費制度ですので、なるべく早めに入会されてフルに活用していただくことをお勧めします。

【年会費】
26400円（消費税込）
翌年の2月15日まで、鴎友進学館のコンテンツに関してすべてご覧、ご利用いただけます。

さらに、WEB会員の皆様には、専任講師がさまざまなご質問にお答えしています。学習方法や併願校の選択などについてもぜひお訊ねください。

お申し込みフォーム

2025年　鴎友学園　第1回　算数4です。

ある小学校の 6 年生 50 人を対象に 10 点満点のテストをしました。このテストの問題は A、B、C の 3 問で、配点は A が 2 点、B が 3 点、C が 5 点です。どの問題も正解か不正解のいずれかです。テストの結果、点数と人数は下の表のようになりました。このテストで正解した問題数が 1 問のみだった人の平均点は 3.1 点でした。問題 C を正解した人は、全部で何人ですか。

【解説と解答】問題はAが2点、Bが3点、Cが5点です。
表からAだけできた人は6人、
Bだけできた人は10人ですが、５点はCだけできるか、AとＢができるか、の2通りあります。1問だけできた人の平均は3.1点ですから、Cだけできた人の数を【1】とすると、
2×６＋３×10＋５×【1】＝3.1×（16＋【1】）
42＋【5】＝49.6＋【3.1】から【1.9】＝7.6　【1】＝4人です。
Cができると、５点、７点、8点、10点をとれるので、Cができたのは
４＋9＋5＋４＝22人です。

（答え）22人

【解説動画】

学さんと友子さんは8時に家を出て、駅に向かいました。学さんは分速250mの速さで走っていましたが、駅に着いたとき忘れ物に気づき、すぐに家へ同じ速さで戻りました。友子さんが一定の速さで歩いていると、その途中で学さんと8時24分にすれ違いました。その後、学さんは家で忘れ物を受け取り、すぐに駅へ分速125 m の速さで向かいました。その結果、学さんと友子さんは同じ時刻に駅に着きました。グラフは、このときの時刻と2人の移動の様子を表したものです。

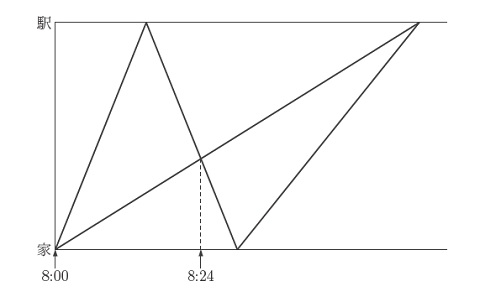
(1)友子さんの歩く速さは分速何mですか。
(2)家から駅までの距離は何mですか。

【解説と解答】

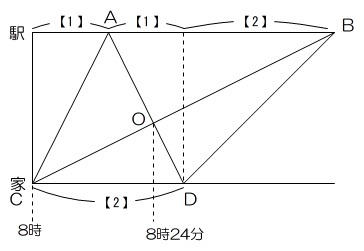
（１）学さんが駅まで行く時間を【1】とすると、家まで帰ってくる時間も【1】。
家から折り返したあとの速さは120ｍと半分になっているので、今度は駅まで【2】の時間がかかります。
それをグラフ上に表すと図のようになります。
ここで学さんと友子さんがすれ違った場所はグラフの三角形ＯＣＤと三角形ＯＡＢの相似から、家から駅までの2/5であることがわかります。学さんは駅まで行ってこの地点までくるのに、
250×24＝6000ｍ走っていますから、家から駅までの距離を<5>とすると、駅からすれ違う場所まで<3>だから
<8>が6000ｍ。<2>は1500ｍ。1500ｍを友子さんは24分で移動するので、
1500÷24＝62.5mです。
（答え）62.5m

（２）（１）から家から駅までは6000÷8×5＝3750ｍ
（答え）3750ｍ

動画解説

2024年　鴎友学園　第2回　算数

図は底面の直径が4cmの円錐です。この円錐に、点Aから側面にそって、OAにたどり着くまで、図のようにひもを巻きつけます。このひもの長さが最も短くなるように巻きつけたとき、たどり着いたOA上の点をBとします。このとき、展開図を考えると、ひもABとOA、OBで囲まれた図形ができます。この図形の面積を求めなさい。

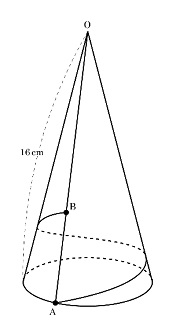
【解説と解答】

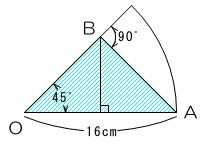
この円錐の母線は16cm、半径は2cmですから、側面のおおぎ形の中心角は360×2/16＝45°になります。
したがってAからBに最短にひもをかけると、ABとOBは直交することになり、OB、OA、ABに囲まれる部分はOA＝16cmの直角二等辺三角形になります。
したがって求める面積は
16×８÷２＝64
（答え）64cm２

2024年　鴎友学園第2回　算数2です。

ある工場に、クッキーを作る機械AとBがあります。Aは1分間に30個、Bは1分間に40個のクッキーを作ることができます。 A、 Bがクッキーを作る速さはそれぞれ一定です。
ある日、クッキーの注文を受けたため、AとBを同時に1台ずつ使ってクッキーを作り 始めました。しかし、途中でBが止まってしまったので、A1台のみで作りました。Bは止まってから1時間後に再び動き始めました。その後はAとBのどちらも止まることなくクッキーを作り続けたところ、Aのみを同時に2台使って同じ数のクッキーを作るときよりも、15分早く注文された数を作り終えることができました。注文されたクッキーの個数を求めなさい。

【解説と解答】

AとBでクッキーを作るときは1分間に70個、Bが止まっていたときは1分間に30個作っています。Bが止まっていた時間は1時間なので、
クッキーができた時間を【1】分とすると、できたクッキーの数は
70×【1】－40×60と表されます。
一方A２台で焼くと【1】よりも15分多くかかるので、できるクッキーの数は60×（【1】＋15）＝【60】＋900
したがって【70】－2400＝【60】＋900
【10】＝3300　【1】＝330分
注文された個数は
70×330－2400＝23100－2400＝20700
（答え）20700個

2024年　第2回　算数6番です。

姉はP地点とQ地点の間を、妹はP地点とR地点の間を往復しました。P地点とQ地点は3600m離れています。また、R地点は、P地点とQ地点の途中にあって、P地点から2400m離れています。
姉は9時にP地点を出発し、自転車を使って時速24kmの速さで、休まずに3往復しました。また、妹は9時にP地点を出発し、時速12kmの速さで走り、R地点に向かいました。妹がR地点に到着すると同時に、P地点に向かう姉がR地点を通過しました。その後、妹はひと休みし、姉が再びR地点を通過すると同時に、P地点に向かって歩いて戻ったところ、3往復を終える姉と同時にP地点に着きました。グラフは姉と妹の移動の様子を表したものです。

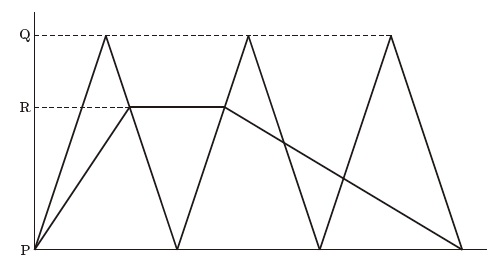
(1) 妹はひと休みした後、時速何kmの速さで歩きましたか。
(2) 妹がR地点からP地点へ歩いているとき、Q地点に向かう姉と出会った時刻を求めなさい。

【解答と解説】
（１）PR間は2400mですから、妹の分速が12000÷60＝200mなので、2400÷200＝12分でRに着きます。
姉の分速は24000÷60＝400m。
PQ間は3600m。
したがって姉が2往復目にRに、Pから到着するまでに、
姉は3600×２＋2400＝9600m移動していますから、
9600÷400＝24分かかります。
姉は3往復するのに、3600×６÷400＝54分かかるので、妹はRからPに戻るのに54－24＝30分かかることになります。
したがって時速は、2400÷30×60÷1000＝4.8

（答え）時速4.8km

（２）姉が2回目にQに戻ってくるのは、3600×４÷400＝36分後です。
その時までに、妹はRを出発してから、80×（36―24）＝960m移動しているので、2人の間の距離は2400－960＝1440m
1440÷（400＋80）＝３分後ですから、36＋３＝3９分後
したがって9時＋39分＝9時39分

（答え）9時39分

2024年　第2回　算数3番です。

次のような規則で逆三角形型に整数を並べます。
　　・１行目には、連続する４つの整数を左から小さい順に並べます。
　　・１行目の左から１番目と２番目の整数の和を、２行目の左から１番目の整数と決めます。
　　・同じようにして、１行目の左から２番目と３番目の整数の和を、２行目の左から２番目の整数と決めます。
　　・３行目、４行目も同じようにして整数を決めます。
１行目の左から１番目の整数がＸのとき、４行目の整数を【X】と表します。
　　　例えば、１行目の左から１番目の整数が２のとき、４行目の整数が28なので、【2】＝28です。

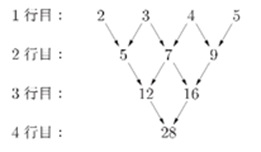
（1）　【1】と【3】をそれぞれ求めなさい。
（2）【1】十【2】十【3】十‥･と【1】から【20】までたしたとき、その和を求めなさい。

【解説と解答】
（１）下図の通りになります。

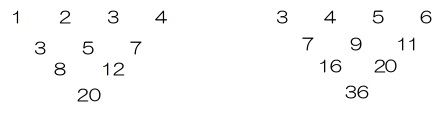
【1】＝20　【3】＝36
（答え）【1】＝20　【3】＝36

（２）それぞれ【X】は1段目の合計の2倍になっています。
したがって【1】＝（１＋４）×４÷２×２＝20
【2】＝（２＋５）×４÷２×２＝28
【3】＝（３＋６）×４÷２×２＝36から
８ずつ増えていることがわかるので
【20】＝20＋８×（20－1）＝172
【20】は（20＋23）×４÷２×２＝172でも求められます。
（20＋172）×20÷２＝1920
（答え）1920

【動画解説】