2025年　鴎友学園　第1回　算数4です。

ある小学校の 6 年生 50 人を対象に 10 点満点のテストをしました。このテストの問題は A、B、C の 3 問で、配点は A が 2 点、B が 3 点、C が 5 点です。どの問題も正解か不正解のいずれかです。テストの結果、点数と人数は下の表のようになりました。このテストで正解した問題数が 1 問のみだった人の平均点は 3.1 点でした。問題 C を正解した人は、全部で何人ですか。

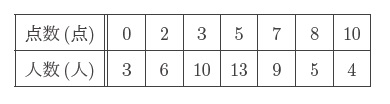
【解説と解答】問題はAが2点、Bが3点、Cが5点です。
表からAだけできた人は6人、
Bだけできた人は10人ですが、５点はCだけできるか、AとＢができるか、の2通りあります。1問だけできた人の平均は3.1点ですから、Cだけできた人の数を【1】とすると、
2×６＋３×10＋５×【1】＝3.1×（16＋【1】）
42＋【5】＝49.6＋【3.1】から【1.9】＝7.6　【1】＝4人です。
Cができると、５点、７点、8点、10点をとれるので、Cができたのは
４＋9＋5＋４＝22人です。

（答え）22人

【解説動画】

学さんと友子さんは8時に家を出て、駅に向かいました。学さんは分速250mの速さで走っていましたが、駅に着いたとき忘れ物に気づき、すぐに家へ同じ速さで戻りました。友子さんが一定の速さで歩いていると、その途中で学さんと8時24分にすれ違いました。その後、学さんは家で忘れ物を受け取り、すぐに駅へ分速125 m の速さで向かいました。その結果、学さんと友子さんは同じ時刻に駅に着きました。グラフは、このときの時刻と2人の移動の様子を表したものです。

(1)友子さんの歩く速さは分速何mですか。
(2)家から駅までの距離は何mですか。

【解説と解答】

（１）学さんが駅まで行く時間を【1】とすると、家まで帰ってくる時間も【1】。
家から折り返したあとの速さは120ｍと半分になっているので、今度は駅まで【2】の時間がかかります。
それをグラフ上に表すと図のようになります。
ここで学さんと友子さんがすれ違った場所はグラフの三角形ＯＣＤと三角形ＯＡＢの相似から、家から駅までの2/5であることがわかります。学さんは駅まで行ってこの地点までくるのに、
250×24＝6000ｍ走っていますから、家から駅までの距離を<5>とすると、駅からすれ違う場所まで<3>だから
<8>が6000ｍ。<2>は1500ｍ。1500ｍを友子さんは24分で移動するので、
1500÷24＝62.5mです。
（答え）62.5m

（２）（１）から家から駅までは6000÷8×5＝3750ｍ
（答え）3750ｍ

動画解説

2024年　鴎友学園　第2回　算数

図は底面の直径が4cmの円錐です。この円錐に、点Aから側面にそって、OAにたどり着くまで、図のようにひもを巻きつけます。このひもの長さが最も短くなるように巻きつけたとき、たどり着いたOA上の点をBとします。このとき、展開図を考えると、ひもABとOA、OBで囲まれた図形ができます。この図形の面積を求めなさい。

【解説と解答】

この円錐の母線は16cm、半径は2cmですから、側面のおおぎ形の中心角は360×2/16＝45°になります。
したがってAからBに最短にひもをかけると、ABとOBは直交することになり、OB、OA、ABに囲まれる部分はOA＝16cmの直角二等辺三角形になります。
したがって求める面積は
16×８÷２＝64
（答え）64cm２

2024年　鴎友学園第2回　算数2です。

ある工場に、クッキーを作る機械AとBがあります。Aは1分間に30個、Bは1分間に40個のクッキーを作ることができます。 A、 Bがクッキーを作る速さはそれぞれ一定です。
ある日、クッキーの注文を受けたため、AとBを同時に1台ずつ使ってクッキーを作り 始めました。しかし、途中でBが止まってしまったので、A1台のみで作りました。Bは止まってから1時間後に再び動き始めました。その後はAとBのどちらも止まることなくクッキーを作り続けたところ、Aのみを同時に2台使って同じ数のクッキーを作るときよりも、15分早く注文された数を作り終えることができました。注文されたクッキーの個数を求めなさい。

【解説と解答】

AとBでクッキーを作るときは1分間に70個、Bが止まっていたときは1分間に30個作っています。Bが止まっていた時間は1時間なので、
クッキーができた時間を【1】分とすると、できたクッキーの数は
70×【1】－40×60と表されます。
一方A２台で焼くと【1】よりも15分多くかかるので、できるクッキーの数は60×（【1】＋15）＝【60】＋900
したがって【70】－2400＝【60】＋900
【10】＝3300　【1】＝330分
注文された個数は
70×330－2400＝23100－2400＝20700
（答え）20700個

2024年　第2回　算数6番です。

姉はP地点とQ地点の間を、妹はP地点とR地点の間を往復しました。P地点とQ地点は3600m離れています。また、R地点は、P地点とQ地点の途中にあって、P地点から2400m離れています。
姉は9時にP地点を出発し、自転車を使って時速24kmの速さで、休まずに3往復しました。また、妹は9時にP地点を出発し、時速12kmの速さで走り、R地点に向かいました。妹がR地点に到着すると同時に、P地点に向かう姉がR地点を通過しました。その後、妹はひと休みし、姉が再びR地点を通過すると同時に、P地点に向かって歩いて戻ったところ、3往復を終える姉と同時にP地点に着きました。グラフは姉と妹の移動の様子を表したものです。

(1) 妹はひと休みした後、時速何kmの速さで歩きましたか。
(2) 妹がR地点からP地点へ歩いているとき、Q地点に向かう姉と出会った時刻を求めなさい。

【解答と解説】
（１）PR間は2400mですから、妹の分速が12000÷60＝200mなので、2400÷200＝12分でRに着きます。
姉の分速は24000÷60＝400m。
PQ間は3600m。
したがって姉が2往復目にRに、Pから到着するまでに、
姉は3600×２＋2400＝9600m移動していますから、
9600÷400＝24分かかります。
姉は3往復するのに、3600×６÷400＝54分かかるので、妹はRからPに戻るのに54－24＝30分かかることになります。
したがって時速は、2400÷30×60÷1000＝4.8

（答え）時速4.8km

（２）姉が2回目にQに戻ってくるのは、3600×４÷400＝36分後です。
その時までに、妹はRを出発してから、80×（36―24）＝960m移動しているので、2人の間の距離は2400－960＝1440m
1440÷（400＋80）＝３分後ですから、36＋３＝3９分後
したがって9時＋39分＝9時39分

（答え）9時39分

2024年　第2回　算数3番です。

次のような規則で逆三角形型に整数を並べます。
　　・１行目には、連続する４つの整数を左から小さい順に並べます。
　　・１行目の左から１番目と２番目の整数の和を、２行目の左から１番目の整数と決めます。
　　・同じようにして、１行目の左から２番目と３番目の整数の和を、２行目の左から２番目の整数と決めます。
　　・３行目、４行目も同じようにして整数を決めます。
１行目の左から１番目の整数がＸのとき、４行目の整数を【X】と表します。
　　　例えば、１行目の左から１番目の整数が２のとき、４行目の整数が28なので、【2】＝28です。

（1）　【1】と【3】をそれぞれ求めなさい。
（2）【1】十【2】十【3】十‥･と【1】から【20】までたしたとき、その和を求めなさい。

【解説と解答】
（１）下図の通りになります。

【1】＝20　【3】＝36
（答え）【1】＝20　【3】＝36

（２）それぞれ【X】は1段目の合計の2倍になっています。
したがって【1】＝（１＋４）×４÷２×２＝20
【2】＝（２＋５）×４÷２×２＝28
【3】＝（３＋６）×４÷２×２＝36から
８ずつ増えていることがわかるので
【20】＝20＋８×（20－1）＝172
【20】は（20＋23）×４÷２×２＝172でも求められます。
（20＋172）×20÷２＝1920
（答え）1920

【動画解説】

2024年　第1回　算数6番です。

図のような台形ABCDがあります。

BE：EF：FG：GC=2：1：2：3です。また、AGとDCは平行です。
(1)AH：HK：KCを、最も簡単な整数の比で表しなさい。
(2)台形ABCDの面積が15cm2のとき、四角形HIJKの面積を求めなさい。

【解説と解答】
（１）AGとDCが平行なのでAD＝GC
BE＝【2】とすると、EF＝【1】、FG＝【2】、GC＝【3】、AD＝【3】
三角形AHDと三角形HECの相似から、
AD：EC＝【3】：（【1】＋【2】＋【3】）＝３：６＝１：２＝AH：HC
三角形AKDと三角形KFCの相似から、
AD：FC＝【3】：（【2】＋【3】）＝３：５＝AK：KC
AC＝24とするとAH＝８　AK＝９　KC＝15から
AH：HK：KC＝８：１：15
（答え）８：１：15

（２）三角形AIDと三角形IEGの相似から、
AD：EG＝【3】：【1】＋【2】＝1：1＝AI：IG
三角形AJDと三角形ＪＦＧの相似から、AD：FG＝【３】：【2】＝３：２＝AJ：JG
AG＝１０とするとAI＝５、AJ＝６　JG＝４より
AI：IJ：JG＝５：１：４
台形ABCD＝15cm2のとき、
三角形ADC＝三角形AGC＝15÷（２＋１＋２＋３＋３）×３＝
四角形HIJK＝三角形AJK－三角形AIH
＝×（×－×）
＝×（－）
＝×＝

（答え）cm２

2024年　第1回　算数2番です。

図の平行四辺形ABCDを､CEを折り目として折ったとき､点Bが移る点をFとします｡このとき､辺ADとCFは交わり､交わった点をGとします｡
辺CDとCGの長さは等しく､角DCGの大きさが42度のとき､角AEFの大きさを求めなさい｡

【解説と解答】

CG＝CD、角DCG＝42°なので、三角形CGDは二等辺三角形だから、〇＝（180－42）÷２＝69°
平行四辺形ABCDだから、角DCB＝角DAE＝180－69＝111°
三角形EBCと三角形EFCは合同になるので、
三角形HGFも底角が〇の二等辺三角形だから、
角FHG＝角AHE＝42°
したがって
角AEH＝180－42－111＝27°

（答え）27°

2024年　鴎友学園　第1回　7です。

学さんと友子さんは毎朝、８時５分にＣ駅に着く電車で通学しています。学さんの家から1100m先にＡ駅があります。Ａ駅から1300m先に友子さんの家があり、その先にＢ駅とＣ駅がこの順にあります。電車はＡ駅を７時52分に発車し、Ｂ駅で２分間停車し、Ｃ駅に８時５分に到着します。Ａ駅からＣ駅までは8.8km離れており、電車の速さは一定です。
　学さんは７時47分に家を出て、Ａ駅で電車に乗り、２駅先のＣ駅まで移動します。友子さんは７時47分に家を出て、Ｂ駅まで自転車で時速16.8kmの速さで向かい、電車に乗ります。
　グラフは、このときの時刻と２人の移動の様子を表したものです。
（1）　友子さんがＢ駅に到着した時刻を求めなさい。
（2）　学さんが家を出た後、母親が忘れ物に気づき、７時52分に家を出て車で時速51kmの速さで追いかけました。途中で自転車に乗った友子さんに出会っだので、友子さんに忘れ物を渡してもらうことにしました。友子さんと学さんの母親が出会った時刻を求めなさい。

【解説と解答】
（１）電車はAB間が6分、BC間が5分でAC間が8.8kmですからAB間は8.8÷（６＋５）×６＝4.8km
A駅から友子さんの家まで1.3kmですから、友子さんの家からB駅まで3.5km。
3.5÷16.8×60＝12.5分。
友子さんは7時47分に家を出るので、B駅に到着するのは7時59分30秒。

（答え）7時59分30秒

（２）学さんの母が家を出たのは、7時52分。そのとき、友子さんはすでに5分走っているので、16.８÷60×５＝1.4km進んでいるから、母との間の距離は1100m＋1300m＋1400m＝3800ｍ
友子さんの分速は280ｍ。学さんのお母さんの分速は51000÷60＝850ｍだから、3800÷（850―280）＝3800÷570＝6分40秒になるので、
7時52分＋6分40秒＝7時58分40秒
（答え）7時58分40秒

2024年第1回　2番です。

Ａさん、Ｂさん、Ｃさんの３人でお金を出しあって、9200円のプレゼントを買います。
　　最初、３人の所持金の比は15：２：８でしたが、ＡさんがＢさんに400円渡し、ＣさんもＢさんにいくらか渡すと、所持金の比は８：３：３になりました。この後、プレゼントを買いました。
（1）　所持金の比が８：３：３になったとき、Ａさんの所持金はいくらになりましたか。
（2）　プレゼントを買った後、３人の所持金の比は５：３：２になりました。Ｃさんがプレゼントを買うために出した金額はいくらですか。

【解説と解答】
（１）最初の3人のお金は15：2：8ですから合計は25です。一方プレゼントを買う前には８：３：３になったので合計14ですから、最初のお金を【350】とするとAさんは【210】あったのが、400円上げたので、【200】になったので【10】＝400円ですから400×20＝8000円
（答え）8000円

（２）プレゼントを買う前にＡさんは8000円、ＢさんとＣさんは3000円になっていました。9200円のプレゼントを買ったので、
8000＋3000×２―9200＝4800円が残りの合計です。
残りは５：３：２ですから、Cさんは4800÷（5＋３＋２）×２＝960円なので、Cさんが出したお金は3000―960＝2040円
（答え）2040円