2025年　洗足学園　第1回　算数４です。

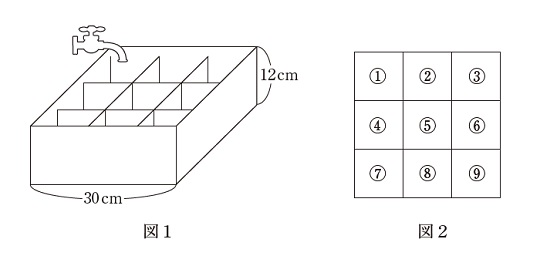
図１のように、1 辺の長さが30 cm の正方形を底面とし、高さが12cm の容器があります。この容器を１辺の長さが10cmの正方形の板を底面に垂直に立てて、図２のように９つのブロックにすき間なく仕切ります。この容器の①のブロックに一定の割合で水を入れていきます。水は、それぞれのブロックの底面から水面までの高さが10cmになると、となり合っている水面の高さが10cm になっていないブロックに同じ割合で流れ込みます。すべてのブロックの水面の高さが10cmになったら水を止めます。水を入れ始めてから2 分で①のブロックの水面の高さが10cm になりました。このとき、次の問いに答えなさい。ただし、水は斜めの位置にあるブロックには流れ込まないものとし、容器や仕切りの板の厚さは考えないものとします。

（1）１つの容器に入る水の量は10×10×10＝1000cm3です。
ここに2分で水が入るのだから、1分あたりは1000÷２＝500cm３です。
①がいっぱいになると②と④にいくので、500÷２＝250
（答え）250cm3

（2）②と④がいっぱいになるのは水が入り始めてから1000÷250＝4分後です。
その後④から⑤と⑦へ、②から③と⑤へ水が入っていきますから、
⑤は250÷２×２＝毎分250cm３ずつ水が入るので、水が入り始めてから
1000÷250＝４分で10cmになりますから、最初からは２＋４＋４＝10分後
（答え）10分後

（３）6分後に⑦に毎分125cm3の水が入り始めますから⑦が満水になるのは
1000÷125＝8分後なので、最初からは14分後です。
したがって⑧には14－10＝4分先に⑤から水が250÷２＝125cm３ずつ入っていくので、4分後には125×４＝500cm3水がはいり、水の高さは
500÷（10×10）＝5cmです。
その後、⑦からは毎分125cm3ずつ、⑤からも125cm3ずつ入っていくので、７cmになるのは10×10×（７－５）÷（125×２）＝0.8分＝48秒。
したがって最初からは14分48秒後。
（答え）14分48秒後