2024年洗足学園第1回の問題です。
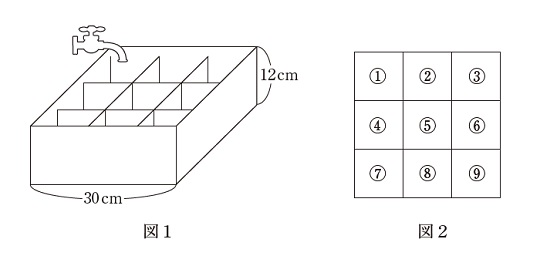
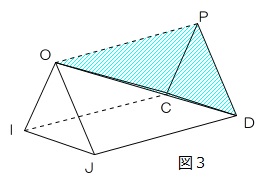
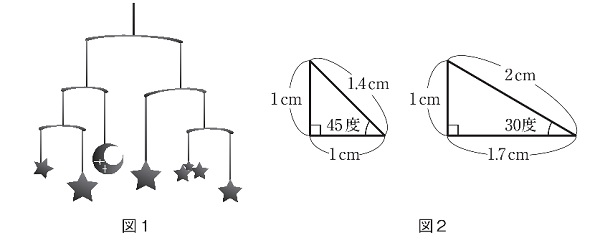
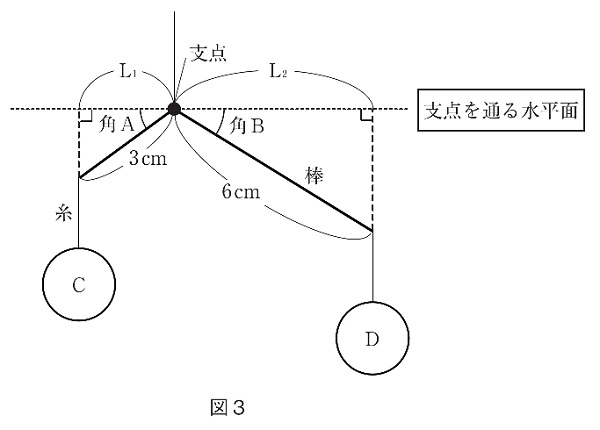
園子さんは、図1のようなモービルのつりあいに興味を持ち、実験をしました。実験で使用する棒や糸の重さや太さは無視できるものとし、棒や円盤はおもりをつるしても、変形したり角度が変化したりしないものとします。また、必要であれば、図2の三角形の対応する辺の長さの比を使用しなさい。小数第2位以下がある場合は、四捨五入して小数第1位まで答えなさい。
【実験1】
図3のように、はしから3cmのところでいろいろな角度に曲げて固定できる9cmの棒の両端に、様々な重さのおもりをつるした。棒が静止したときの角A、角Bの大きさ、おもりC、Dの重さを記録し、その結果を表1にまとめた。図のL1、L2は、支点を通る水平面におもりC、Dをつるしている糸の延長線がぶつかる点と、支点との距離を表している。 L1やL2を『おもりと支点の水平方向の距離』とする。
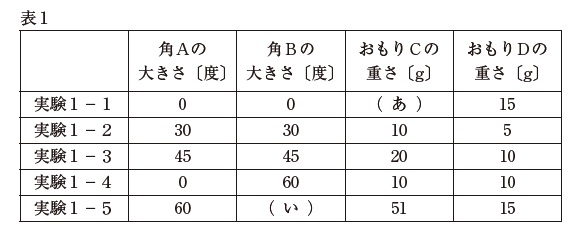
（１） 表１の（あ）に当てはまる数値を答えなさい。
（２） 実験１－２および実験１－３のL1の長さはそれぞれ何cmですか。
（３）【実験１】の結果から園子さんは、棒が静止しているとき、『おもりと支点の水平方向の距離』と『おもりの重さ』に関係があると気づきました。どのような関係があるか、［L1］、［L2］、「重さ」を用いて文章で答えなさい。
（４） 表１の（い）に当てはまる数値を答えなさい。
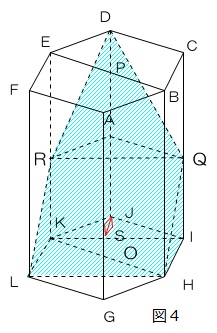
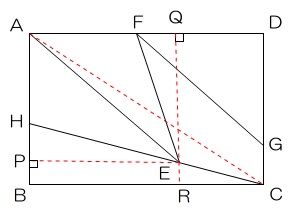
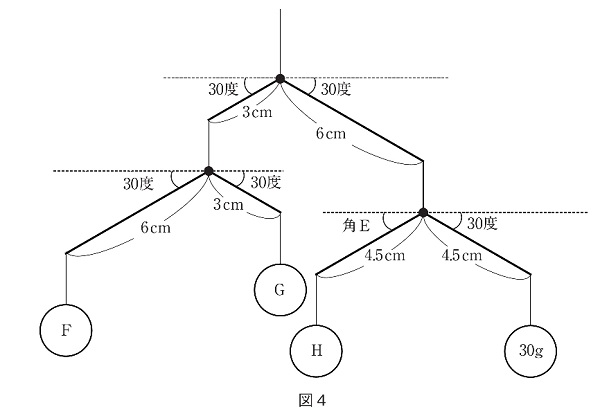
園子さんは【実験1】の結果をもとに、図4のようなモービルをつくりました。棒は【実験1】で使用した棒を2本と、真ん中でいろいろな角度に曲げて固定できる9cmの棒を1本使用しました。
(5) 図4の角Eが次の①、②の角度で静止しているとき、F～Hはそれぞれ何gですか。
① 30度 ② 60度
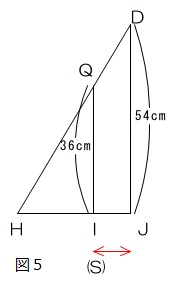
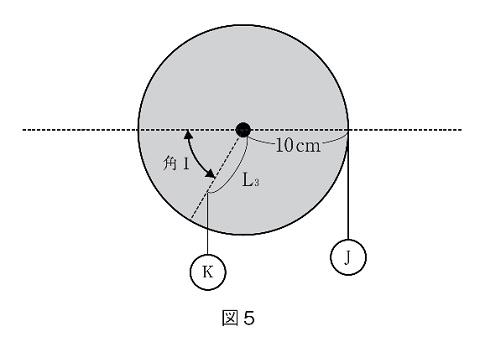
園子さんは図5のように、壁に中心を固定してなめらかに回転できるようにした円盤を用いて同様の実験ができると考えました。円盤の半径を10cmとします。
【実験2】
おもりJを円盤のふちにつるし、おもりJが動かないように、もう1つのおもりKを円盤の中心から長さL3の位置につるした。このときの角Iの大きさ、おもりJ、Kの重さ、L3の長さをはかり、その結果を表2にまとめた。
(6) 表2の(う)、(え)に当てはまる数値を答えなさい。
【解説と解答】
モービルのつりあいは、棒の重さを無視できる場合、支点からの水平距離×重さが等しくなればつりあいます。
（1）角度がともに0°であれば、水平距離はL1＝3cm、L2＝6cmですから、3×（あ）＝6×15＝90より（あ）＝30ｇ
（答え）30g
（2）角度が同じであればL1：L2＝1：2になるので、図2からL1：3＝1.7：2ですからL1＝3×1.7÷2＝2.55≒2.6･･･から2，6cm
これも角度が同じですが、45°ですから、直角二等辺三角形になるのでL1：3＝1：1.4からL1＝3×1÷1.4＝2.14≒2.1cm
（答え）（実験1−2） 2.6cm （実験1−3） 2.1cm
（3）L1×Ｃの重さ＝L2×Dの重さです。
（答え）L1とおもりCの重さの積はL2とおもりDの積に等しい。
（4）51：15＝17：5ですからL1：L2＝5：17です。Aが60°ですから、L1＝3÷2＝1.5cmなので、L2＝5.1cmです。したがって角Bは図2の右側の三角形になり30°です。
（答え）30°
（5）① 角Eが30°であれば、L1＝L2ですからH＝30g その上のモービルにかかる重さは30×2＝60g
上のモービルはL1：L2＝1：2ですから左端にかかる重さは60×2＝120g。それをF：G＝1：2に分けるので、F＝120÷（1＋2）×1＝40g G＝120−40＝80g
（答え）F 40g G 80ｇ H 30g
② 角Eが60°になるとL1；L2＝1:1.7になるので、30×1.7÷1＝51gがH。その上のモービルにかかる重さは51＋30＝81g
このモービルの左端の重さは81×2＝162g 162gをF：G＝1：2に分けるので、F＝162÷（1＋2）×1＝54g G＝162ー54＝108g
（答え）F 54g G 108g H 51g
（6）実験2−1では、重りの比がJ：K＝1：2になっているので、Kの水平距離は5cmです。L3＝10cmですから、2：1になるので角I＝60°です。
実験2−2では、8cmで30°ですから水平距離の比は、図2の右側の三角形と同じで、その比は2：1.7ですから、水平距離は8÷2×1.7＝6.8cmです。
10×17＝6.8×（え）ですから（え）＝170÷6.8＝25g
（答え）（う） 60 （え）25
解説動画
