2024年　洗足学園第2回　算数5でうｓ。

下の図のような底面が正六角形で高さが54cmの正六角柱の密閉された容器があります。

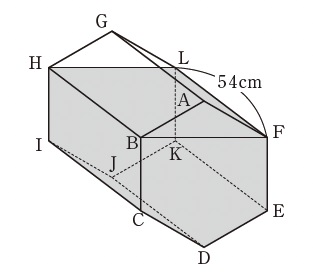
この容器に水が2160cm³ 入っています。いま、この容器を辺BC、FEが水平な床に対して垂直になるように手で支えると、水面が長方形BFLHとなりました。このとき、次の問いに答えなさい。
(1) 底面の正六角形の面積は何cm² ですか。
(2) 水平な床に辺IJがくっつくように容器を傾けて、水面を四角形CDKHにするためには、水を何cm3 捨てればよいですか。
(3) 水平な床から点Jが離れないように容器を傾けて、水面が3 点D、H、Lを通る平面になるようにするためには、(2)の状態から水を何cm3 加えればよいですか。

【解説と解答】
(1) 2160÷54＝40cm2が五角形BCDEFの面積です。

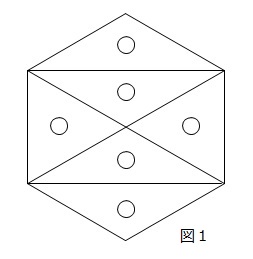
五角形BCDEFは図のように、正六角形ABCDEFの6分の５になるので。
40÷５×6＝48cm²
(答え) 48cm²

(2) 図２の斜線部に水が入ります。Pを正六角形ABCDEFの中心、Oを正六角形GHIJKLの中心とするとPを三角錐HOICと三角錐OJKDは8×54÷３＝144cm³

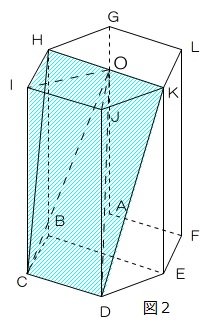
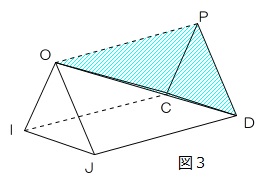
図３のように四角錐OIJDCは三角柱OIJCPDから三角錐CPDOを引くので、合計すると三角柱OIJCPDと三角錐HOICの合計に等しくなるので、144＋8×54＝144＋432＝576ですから、
2160－576＝1584cm³の水を捨てます。
（答え）1584cm³
（３）求める立体は図４の切断三角柱DRKIQと四角柱RKLQIHです。

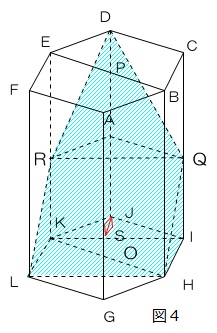
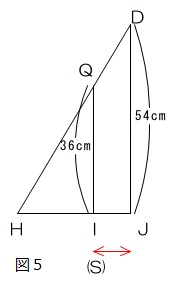
QIは図５のようにJS：IH＝１：２ですから54×2/3＝36cmです。
したがって切断三角柱DRKIQは
８×（54＋36＋36）×1/3＝336
四角柱RKLQIHは８×４×36÷２＝576
336＋576－576＝336cm³足せばよいことになります。
（答え）336cm³