2023年第2回　3－4です。

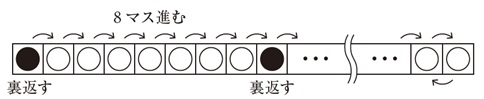
1 列に並んでいる2023個のマス目に、コインを1 枚ずつ置きました。最初に、左端のコインを裏返し、右に8 マス進んだ位置のコインを裏返します。このまま、8 マス進んでコインを裏返すことをくり返し、端に着いたら進む向きを逆にします。ただし、8 マス進む前に端に着いたら、残りの数を折り返して進みます。裏返した回数が2023回のとき、裏面が見えているコインは全部で何枚ですか。ただし、はじめにコインは、すべて表面が見えるように置きました。

【解説と解答】

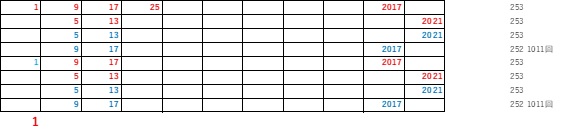
（上図は赤字が裏、青字が表）
左から1番、2番と番号をつけていくと、1番から2023番までが並んでいます。
最初に1番から8で割って1余る数が裏返されるので、最後2017が裏返り、そのあと、2017＋8―2023＝2ですから2023－2＝2021が裏返しになります。
2021は8で割って、5余る数ですから、最後は5が裏返しになります。
そのあと、引き返すとまた5が裏返しになるので、2021まで裏返しになり、すると次は2017が裏返しになり、最後1まで裏返しになります。
そこで2往復目を上図のように9で止めると、1011回裏返しにしています。
次は1が表になって、9以降は裏になりますから、次に1011回裏返しにすると9まで元に戻ります。1は表でしたから、1011×2＋1＝2023回目は1で、これが裏になります。このとき1だけが裏です。

（答え）1枚