AさんとBさんは，山を越えてとなり町まで歩きます。ＡさんはＸ町を出発し頂上で30 分の休けいをとってＹ町へ，ＢさんはＡさんが出発した1 時間後にY 町を出発し，頂上で30 分の休けいをとってＸ町へ行き，ＢさんはＡさんがＹ町へ着く前にＸ町に着きました。
ＡさんとＢさんは，上り道でも下り道でもそれぞれ一定の速さで歩き，上り道では下り道の3/4倍の速さで歩きます。下のグラフは，Ａさんが出発してからの時間とＡさんとＢさんの間の道のりを表しています。このとき，次の問いに答えなさい。

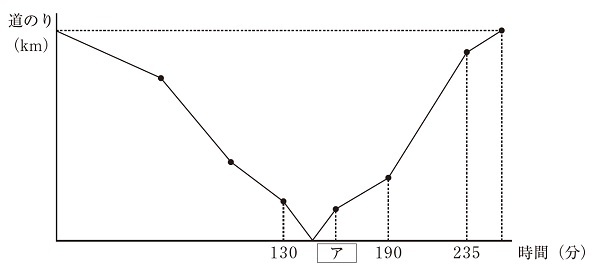
（１） グラフのアにあてはまる数を答えなさい。
（２） ＡさんとＢさんの上り道を歩く速さの比を，最も簡単な整数の比で答えなさい。
（３） ＡさんとＢさんがすれ違った場所をＺ地点とするとき，Ｘ町からＺ地点とＹ町からＺ地点の道のりの比を，最も簡単な整数の比で答えなさい。なお，この問題は解答までの考え方を表す式や文章・図を書きなさい。

【解説と解答】

（１）グラフの最初の点は60分です、グラフが時間の軸に平行になっていないとこから、二人が同時に動いていないところはありません。したがって次の点はどちらかが頂上に到着した点なので、100分となり、130分で出発し、その後アの時間にどちらかが頂上について190分後に出発したことになりますから、アは160分です。
（答え）160
（２）190分でBさんが出発し、235分で到着すると45分ですから、Bさんは同じ距離を上るのに60分かかることになります。130の前の点はAさんが頂上に到着し、130分はAさんが頂上を出発した時間になるので、Aさんが頂上に到着した時間は100分。
したがって速さの比はA：B＝３：５です。
（答え）3：5
（３）Aさんの上りの分速を【3】とすると、下りは【4】ですから、
Xから頂上までは【3】×100＝【300】です。
一方Aさんが頂上を出発するとき、Bさんは70分歩いているので、【5】×70＝【350】のところにいます。Bさんがのぼるのにかかった時間は160－60＝100分ですから、Y町から頂上までは【500】あります。したがってAさんが頂上を出発したとき、二人の距離は【500】－【350】＝【150】で、1分間に【4】＋【5】＝【9】縮まるから、二人がすれ違った場所は【150】÷【9】＝50/3分　だから頂上から
【4】×50/3＝【200/3】下になるので、Yからは【500】－【200/3】＝【1300/3】がZ
Xからは【300】＋【200/3】＝【1100/3】だからXZ：ZY＝11：13
（答え）11：13