2024年第2回　算数4番です。

１を超えない分数を、分母が１であるものから順に、分子も小さい順になるように並べると、以下のようになります。

・・ ・・・・・・・・・・・

このとき、次の問に答えなさい。

（１）分母が455であるような既約分数（それ以上約分できない分数）は何個ありますか。
（２）はじめから455番目の分数を答えなさい。
（３）はじめから455番目までの分数の和はいくつですか。

【解説と解答】
（１）

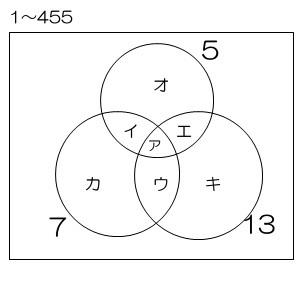
455＝5×７×13ですから、分子が、１～455の中で、５でも７でも13でも割り切れない数が既約分数になります。
455÷５＝91　455÷７＝65　455÷13＝35
455÷35＝13　455÷65＝７　455÷91＝5
から
ア＝１　イ＝13－１＝12　ウ　5－１＝4
エ＝7―１＝６　オ＝91－１―12―６＝72
カ＝65－１－12―4＝48
キ＝35－１－4－6＝24から
１＋12＋4＋6＋72＋48＋24＝167
455－167＝288

（答え）288個

（２）１～30までの和は（１＋30）×30÷2＝465
１～29までの和は（1＋29）×29÷2＝435から
455番目の分数は455－435＝20なのでです。
（答え）

（３）分母が１の分数の和は１、分母が２の分数の和は1.5、分母が3の分数の和は２と0.5ずつ増えていきます。
分母が29の分数は435÷29＝15ですから、ここまで
（１＋15）×29÷２＝232
分母が30の分数は１～20までなので、分子の和は（１＋20）×20÷２＝210
210÷30＝７から232＋７＝239
（答え）239

【解説動画】