投稿者「TanakaTakashi」のアーカイブ

文章題

2025年　鴎友学園　第1回　算数4です。

ある小学校の 6 年生 50 人を対象に 10 点満点のテストをしました。このテストの問題は A、B、C の 3 問で、配点は A が 2 点、B が 3 点、C が 5 点です。どの問題も正解か不正解のいずれかです。テストの結果、点数と人数は下の表のようになりました。このテストで正解した問題数が 1 問のみだった人の平均点は 3.1 点でした。問題 C を正解した人は、全部で何人ですか。

【解説と解答】問題はAが2点、Bが3点、Cが5点です。
表からAだけできた人は6人、
Bだけできた人は10人ですが、５点はCだけできるか、AとＢができるか、の2通りあります。1問だけできた人の平均は3.1点ですから、Cだけできた人の数を【1】とすると、
2×６＋３×10＋５×【1】＝3.1×（16＋【1】）
42＋【5】＝49.6＋【3.1】から【1.9】＝7.6　【1】＝4人です。
Cができると、５点、７点、8点、10点をとれるので、Cができたのは
４＋9＋5＋４＝22人です。

（答え）22人

【解説動画】

速さに関する問題

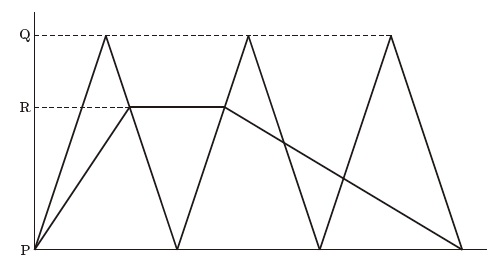
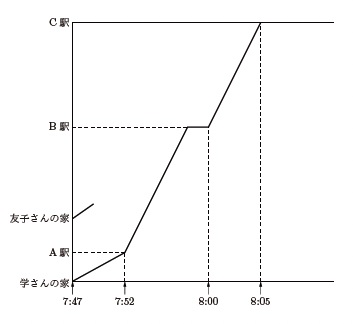
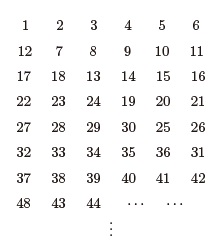
学さんと友子さんは8時に家を出て、駅に向かいました。学さんは分速250mの速さで走っていましたが、駅に着いたとき忘れ物に気づき、すぐに家へ同じ速さで戻りました。友子さんが一定の速さで歩いていると、その途中で学さんと8時24分にすれ違いました。その後、学さんは家で忘れ物を受け取り、すぐに駅へ分速125 m の速さで向かいました。その結果、学さんと友子さんは同じ時刻に駅に着きました。グラフは、このときの時刻と2人の移動の様子を表したものです。

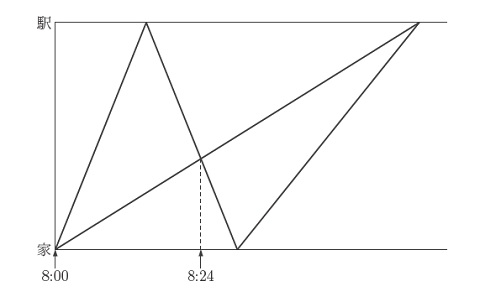
(1)友子さんの歩く速さは分速何mですか。
(2)家から駅までの距離は何mですか。

【解説と解答】

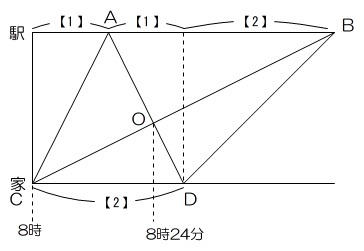
（１）学さんが駅まで行く時間を【1】とすると、家まで帰ってくる時間も【1】。
家から折り返したあとの速さは120ｍと半分になっているので、今度は駅まで【2】の時間がかかります。
それをグラフ上に表すと図のようになります。
ここで学さんと友子さんがすれ違った場所はグラフの三角形ＯＣＤと三角形ＯＡＢの相似から、家から駅までの2/5であることがわかります。学さんは駅まで行ってこの地点までくるのに、
250×24＝6000ｍ走っていますから、家から駅までの距離を<5>とすると、駅からすれ違う場所まで<3>だから
<8>が6000ｍ。<2>は1500ｍ。1500ｍを友子さんは24分で移動するので、
1500÷24＝62.5mです。
（答え）62.5m

（２）（１）から家から駅までは6000÷8×5＝3750ｍ
（答え）3750ｍ

動画解説

立体図形に関する問題

2024年　鴎友学園　第2回　算数

図は底面の直径が4cmの円錐です。この円錐に、点Aから側面にそって、OAにたどり着くまで、図のようにひもを巻きつけます。このひもの長さが最も短くなるように巻きつけたとき、たどり着いたOA上の点をBとします。このとき、展開図を考えると、ひもABとOA、OBで囲まれた図形ができます。この図形の面積を求めなさい。

【解説と解答】

この円錐の母線は16cm、半径は2cmですから、側面のおおぎ形の中心角は360×2/16＝45°になります。
したがってAからBに最短にひもをかけると、ABとOBは直交することになり、OB、OA、ABに囲まれる部分はOA＝16cmの直角二等辺三角形になります。
したがって求める面積は
16×８÷２＝64
（答え）64cm２

比と割合に関する問題

2024年　鴎友学園第2回　算数2です。

ある工場に、クッキーを作る機械AとBがあります。Aは1分間に30個、Bは1分間に40個のクッキーを作ることができます。 A、 Bがクッキーを作る速さはそれぞれ一定です。
ある日、クッキーの注文を受けたため、AとBを同時に1台ずつ使ってクッキーを作り 始めました。しかし、途中でBが止まってしまったので、A1台のみで作りました。Bは止まってから1時間後に再び動き始めました。その後はAとBのどちらも止まることなくクッキーを作り続けたところ、Aのみを同時に2台使って同じ数のクッキーを作るときよりも、15分早く注文された数を作り終えることができました。注文されたクッキーの個数を求めなさい。

【解説と解答】

AとBでクッキーを作るときは1分間に70個、Bが止まっていたときは1分間に30個作っています。Bが止まっていた時間は1時間なので、
クッキーができた時間を【1】分とすると、できたクッキーの数は
70×【1】－40×60と表されます。
一方A２台で焼くと【1】よりも15分多くかかるので、できるクッキーの数は60×（【1】＋15）＝【60】＋900
したがって【70】－2400＝【60】＋900
【10】＝3300　【1】＝330分
注文された個数は
70×330－2400＝23100－2400＝20700
（答え）20700個