2022年　第2回の出題です。

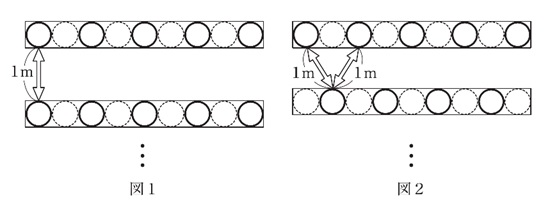
体育館で学年集会を行うことになりました。９人がけの長いすを使って、全員が前から順に着席していきます。ただし人と人の間隔を１メートル以上空ける必要があるため、９人がけの長いすには１つおきにしか座れません。図１のように５人ずつ座ると長いすの数が少なくてすみますが、図２のように前から５人、４人、５人、…と交互に座ると長いすと長いすの間隔をせまくできます。このとき、次の問いに答えなさい。

（１）学年の生徒数が240人のとき、図２のように座ると、図１のときに比べて長いすは何脚多く必要ですか。
（２）学年の生徒数が（　　　）人のとき、図１のときと図２のときの長いすの数の差が３脚で、どちらも最後列の長いすに座る人数が４人でした。（　　　）に入る数として考えられるものをすべて答えなさい。
（３）図１のときと図２のときの長いすの数の差が４脚のとき、考えられる生徒数として最も少ないのは何人ですか。

【解説と解答】
（１）240人の場合、図１のようにすわると長椅子は240÷5＝48脚いります。
一方図２の場合は240÷9＝26.…6ですから、２×26＋２＝54脚いります。
54－48＝６脚
（答え）６脚
（２）図１のときの長椅子の数を【1】とすると、
生徒の数は5×【1】－１＝【5】－１となります。
図２の場合、最後の長椅子が4人ですが、それが（ア）5人がけの場合と（イ）4人がけの場合で違います。
（ア）人数は（【1】＋２）÷２×9＋４＝【4.5】＋13
（イ）人数は（【1】＋３）÷２×9＝【4.5】＋13.5
（ア）の時【5】－１＝【4.5】＋13から【0.5】＝14　【1】＝28となるので、
人数は28×5―１＝139人
（イ）のときは【4.5】＋13.5＝【5】－１　【0.5】＝14.5から【1】＝29となるので、29×５－1＝144人
（答え）139人、144人
（３）図２の座り方で、図１の座り方との差が一番小さくなることを考えます。
図１の座り方ですべての椅子が5人がけになったとき、図２の座り方ではそれより４つ椅子が多いので、
（ウ）図１の座り方が奇数の場合
残りの４つの椅子は４＋５＋４＋１＝14人が最小になります。
（エ）図１の座り方が偶数の場合
残りの４つの椅子は5＋４＋５＋１＝15人が最小になります。
（ウ）２つの椅子で1人の差ができるので、14人の差ができるのは
図１の座り方で２×14＋１＝29脚　このとき図１の座り方では145人、図２の座り方でも（29＋1）÷２×9＋５＋４＋１＝135＋10＝145人になります。
（エ）15人の差ができるので、図１の座り方でいすの数は15×２＝30脚になるので、
図１の座り方で５×30＝150人　図２の座り方で9×30÷２＋15＝150人
したがって一番少ない人数は145人
（答え）145人