洗足の算数の出題パターンはある程度決まっています。
1が計算問題2題。
2が小問4題。
3が小問4題。
そして4.5が大問。
2と3は小問が4題ですが、やはりレベル差があります。下は2023年第3回の小問2-2。
下の図の点線は正方形のそれぞれの辺の真ん中の点を結んでいます。このとき、色のついた部分の面積は正方形全体の面積の何倍ですか。
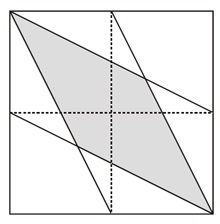
なんとなく面倒な感じはしますが、これは2番なので、それほど難しくないと考えられれば、あっという間に解けるでしょう。
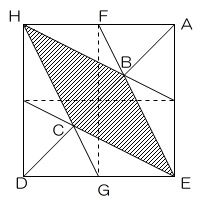
図のようにAからDに線を引くと、AB:BD=1:2、またAC:CD=2:1より AB:BC;CD=1:1:1です。
したがって三角形BCEは三角形ADEの1/3ですから、斜線部も正方形全体の1/3になります。
解説だとこうなりますが、あっという間に気づいた子も多かったでしょう。2と3にはそれなりにレベル差がありますから、これは簡単に解けるはず、という考えは持っていて良いと思います。
