2024年第1回　算数　3の（2）です。

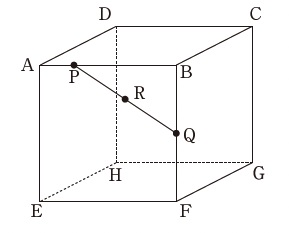
立方体ABCDEFGHがあります。辺AB上にAP：PB＝１：３となる点を、辺BF上にBQ：QF＝１：１となる点Qをとります。また、点Pと点Qを結んだ直線上に点Rをとります。三角形RQGの面積は、３点P、Q、Gを通る平面で立方体をきったときの切り口の面積の1/3倍になりました。このとき、PRとRQの長さの比を最も簡単な整数で答えなさい。

【解説と解答】
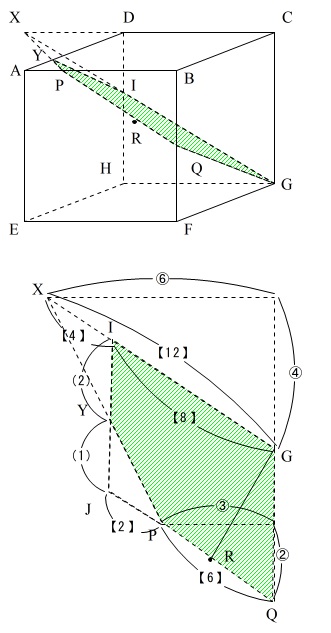
図のようにPQGの平面が切れますので、切り口は緑の部分になります。
立方体の一辺を④とすると、PB＝③
BQ＝②ですから、XC：CG＝３：２なのでXC＝⑥、XD＝②　AP＝①ですから
AY：YD＝１：２になります。
下図は、それを垂直な線上から見た図です。このとき、IJQGは平行四辺形になります。JY：YI＝AY：YD＝１：２でJはPQとAEを延長した交点です。
全体の平行四辺形に対して、三角形YJPは1/2×1/3×1/4＝1/24ですから、緑色の部分は、平行四辺形の１－1/24＝23/24
三角形RQGはその3分の1なので23/72
三角形PQGの面積は1/2×3/4＝3/8ですから
三角形PRGは3/8－23/72＝4/72となるので、
PR：RQ＝4：23
（答え）４：23