2024年　第1回の問題です。

AからBまでは上り坂、BからCまでは平らな道、CからDまでは下り坂となっている登山コースがあります。花子さんはA地点から、よし子さんはD地点から同時に出発したところ、1時間45分後に花子さんが平らな道をだけ進んだところで2人は出会いました。また、花子さんがD地点に着いた5分後によし子さんがA地点に着きました。 2 人はどちらも上り坂を時速 1.5km、平らな道を時速 3km、下り坂を時速2kmで進みます。このとき、次の問いに答えなさい。
(1)よし子さんが B 地点に着いたのは、花子さんがC地点に着いてから何分後ですか。
(2)花子さんが A 地点を出発してからD地点に着くまでに何時間何分かかりましたか。
(3)2 人はしばらく休んだ後、再び同時に出発し、来た道を戻りました。しかし、途中で雨が降り始めたため、すぐに花子さんは残りの上り坂と平らな道を進む速さだけ倍にしました。また、よし子さんは下り坂を進む速さだけ倍にしたところ、花子さんがA地点に着くと同時によし子さんがD地点に着きました。 雨が降り始めたのは2人が再び出発してから何分後ですか。

【解説と解答】
（１）

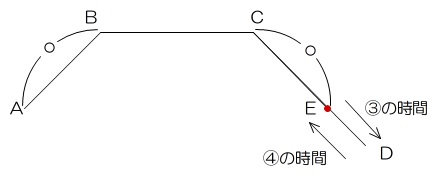
二人とも上り、下り、平地での速さは同じです。したがってAからBまでとCからDまでの距離が同じであれば、BCの中央で出会いますが、BからBCの5/6で出会っているので、CDの方がABよりも長いことがわかります。ABとCDの差（図のEDの距離）を花子さんは下り、よしこさんは上りますから、1.5：２＝３：４なので、かかる時間は花子さん：よし子さん＝３：４です。この差が5分ですから、花子さんは15分で下るので、２×＝0.5kmがEDの距離になります。0.5kmをよし子さんがのぼるのに0.5÷1.5×60＝20分かかるので、よし子さんがCに着くのは、花子さんがBに着いてから20分後です。したがってよし子さんは花子さんがＣについてから20分後にＢに着きます。
（答え）20分後
（２）BC間を【6】とすれば、出会うまでに花子さんは【5】、よし子さんは【1】動いているので、花子さんは【4】の距離を20分で移動したことになるから、【6】の距離は20÷４×６＝30分かかります。
花子さんはBから出会うまでに25分かかるので、AからBまで1時間45分－25分＝1時間20分ですから、ABは1.5×＝2kmです。
CDは２＋0.5＝2.5kmですから、2.5÷２＝1.25＝1時間15分かかるので、1時間20分＋30分＋1時間15分＝3時間5分

（答え）3時間5分
（3）速さが変わった後は、花子さんは上りが1.5×＝1.8km、
平地が3×＝3.6kmです。よし子さんは下りが２×＝2.5kmです。
よし子さんがCからDに下るのはすべて時速2.5kmですから、2.5÷2.5＝1時間。２÷1.5＋30分＋1時間ですから、2時間50分かかっています。
花子さんはABを下るのが２÷２＝1時間、平地が1.5÷3.6×60＝25分ですから、DからCに上るのに2時間50分－1時間－25分＝1時間25分＝時間です。CD間は2.5kmですから
（1.8×－2.5）÷（1.8－1.5）＝時間＝10分が1.5kmで動いた時間です。
（答え）10分後

【解説動画】