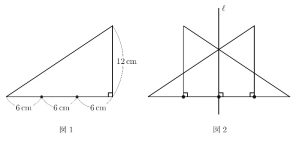
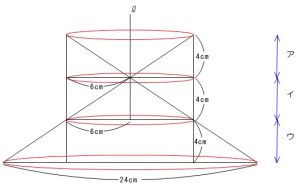
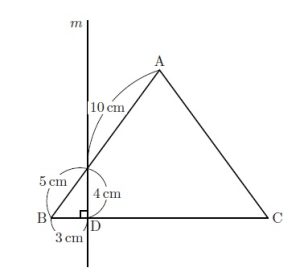
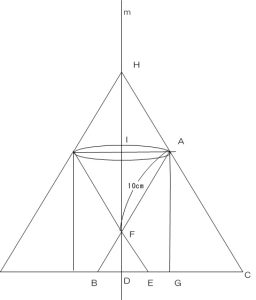
2024年 第1回4番の問題です。
整数をある規則にしたがって、次のように並べました。例えば、左から3番目、上から4番目の整数は24です。
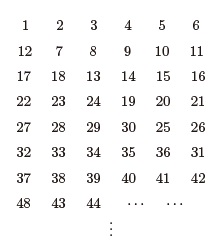
(1)左から2番目、上から100番目の数は何ですか。
(2)2024は左から何番目、上から何番目ですか。
【解説と解答】
(1) 6個ずつ並んでいますが、1つのグループで一番小さい数が左から1つずつずれていき、1つのグループの一番小さい数が一番左に戻るのは7番目になります。(上から7番目は37から始まり、一番小さい数が一番左に来ています。)
100番目は6×99=594ですから595から600までです。
100÷6=16…4から一番小さい数は左から4番目にいるので、
595、596、597、598、599、600が
598、599、600、595、596、597と並びますから、左から2番目は599です。
(答え)599
(2)2024は2024÷6=337・・・2から338番目のグループなので、
2023、2024、2025、2026、2027、2028となり、また2余るので、
一番小さい数は左から2番目にくるから、
2028、2023、2024…となるので、左から3番目、上から338番目です。
(答え)左から3番目、上から338番目