（１）　真っ暗な部屋で、日光のもとでは白く見える壁に、赤色、青色、緑色の光を図１のように当てたところ、２つの光が重なったところはそれぞれ、赤紫色、黄色、空色に見えました．３つの光が重なったところは、何色に見えますか。適当なものを次より１つ選び、記号で答えなさい。

　　　　　ア．黒色　　　イ．白色　　　ウ．褐色　　　エ．灰色

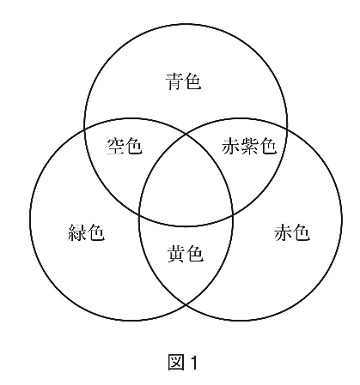
（２）　真っ暗な部屋で、日光のもとでは赤く見える紙に、赤紫色の光を当てると、赤く見えました。当てる光を空色にすると、光が当たっているのに暗いままでした。

　　　①　この結果から分かる、赤い紙の光に対する性質を説明しなさい。

　　　②　真っ暗な部屋で、ある色の壁に色々な光を当てました。壁は、赤色の光を当てると赤色に見え、緑色の光を当てると緑色に見え、青色の光を当てると暗いままでした。この壁は日光のもとでは何色に見えると考えられますか。適当なものを次より１つ選び、記号で答えなさい。

　　　　　　ア．赤色　　　　　　　イ．青色　　　　　　ウ．緑色
　　　　　　エ．赤紫色　　　　　　オ．黄色　　　　　　カ．空色

（３）　図２のように、中央に直径３mmの円形の穴をあけた厚紙を用意し、日光のもとでは白く見えるスクリーンの30cm手前に置きました。厚紙の30cm手前で穴と同し高さから懐中電灯で赤色の光を当てると、厚紙とスクリーンに赤い部分ができました。ただし、厚紙とスクリーンは十分大きく、光がはみ出すことはないものとします。

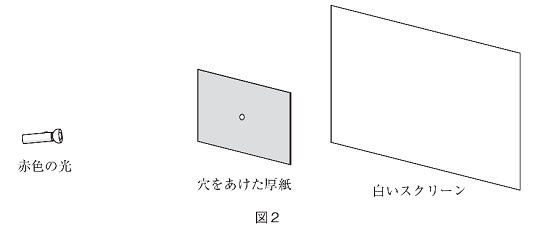
①スクリーンにできた赤い部分の面積は何㎜2ですか。答えは、小数第３位以下があるときは四捨五入して小数第２位まで求めなさい。ただし、円周率は3.14とします。

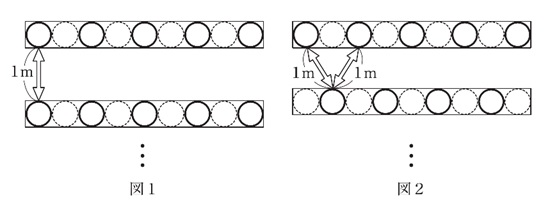
②図２の状態から、厚紙の穴の３cm上に同し形、大きさの穴をあけ、図３のようにその穴と同し高さから青色の光も当てました。すると、スクリーン上には明るい部分が４か所できました。それぞれの色を上から順番に、次より１つずつ選び、記号で答えなさい。ただし、同し記号を何度選んでも良いものとします。

　　　ア. 赤色　　　　　　　イ. 青色　　　　　　ウ. 緑色
　　　エ. 赤紫色　　　　　　オ. 黄色　　　　　　カ. 空色

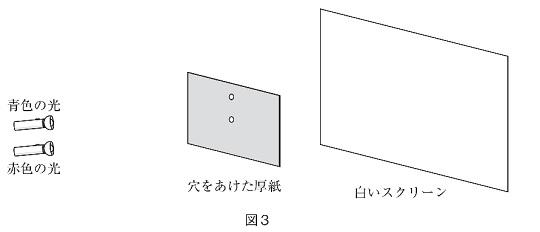
③図３の状態からさらに、厚紙のはじめの穴から３cm下にも同じ形、大きさの穴をあけ、その穴と同じ高さから緑色の光も当てると、スクリーン上には明るい部分が７か所できました．上から２番目、７番目の色を次より１つずつ選び、記号で答えなさい．ただし、同し記号を何度選んでも良いものとします。

　　　　ア．赤色　　　　　　　イ．青色　　　　　　ウ．緑色
　　　　エ．赤紫色　　　　　　オ．黄色　　　　　　力．空色

④スクリーンを日光のもとでは赤く見えるものに変えて、真っ暗な部屋で③と同様に赤色、青色、緑色の光を当てると、スクリーン上に明るい部分は何か所できますか。

（４）　ヒトは３色の光の組み合わせで色を判別しており、これを３色型色覚といいます。生物によって、何色の光の組み合わせを用いているかが異なります。

①多くのほ乳類は２色型色覚で、２色の光の組み合わせで色を判別しています。ヒトが識別できる色でも、赤色と緑色の光の組み合わせで色を判別している生物には識別できない色があります。この生物が識別できない色の組み合わせとして適当なものを次よりすべて選び、記号で答えなさい．

　　　　ア．赤色と赤紫色　　　イ．赤色と黄色　　　ウ．赤色と空色
　　　　エ．緑色と赤紫色　　　オ．緑色と黄色　　　カ．緑色と空色
　　　　キ．赤紫色と黄色　　　ク．黄色と空色　　　ケ．空色と赤紫色
②ハチドリは４色型色覚です。ハチドリの色の見え方について、適当なものを次より１つ選び、記号で答えなさい。

　　　　ア．ヒトにとって真っ暗な場所は、ハチドリにとっても真っ暗である。
　　　　イ．２つの物体の色を比べる時、ヒトが識別できなければ、ハチドリにも識別できない。
　　　　ウ．ヒトが識別できる色の数よりも、ハチドリが識別できる色の数は少ない。
　　　　エ．ヒトに無地に見えていても、ハチドリには模様があるように見えるものがある。

【解説と解答】
（１）赤、青、緑が重なると白に見えます。
（答え）　

（２）
①　赤紫が赤に見えることから、青は反射していないことがわかります。また空色の光を当てても暗いままだったことから、緑色も反射していません。したがって答えは赤しか反射しない、です。
（答え）赤色のみ反射する。

②　問題の条件から赤と緑は反射し、青は反射しません。したがって日光のもとでは、赤と緑が混じった黄色に見えることになります。
（答え）オ

（３）
①　光源から穴、穴からスクリーンの距離が１：１です。したがって穴の2倍の直径になるので、
3×3×3.14＝28.26㎜2になります。
（答え）28.26㎜2

②　４つの明るい部分ができたことから、それぞれの穴を通った赤い色と青い色があることになります。下の赤が穴を通って青の上に来ます。
一番上は上の穴を抜けた赤、次が上の穴を抜けた青、次が下の穴を抜けた赤、一番下が下の穴を抜けた青ということになるので、アイアイです。
（答え）アイアイ

③　全部違うのであれば、9つできるはずですから、２つ重なっていることがわかります。ひとつの穴は上から、緑、赤、青となりますから、
緑、赤、青、緑、赤、青、緑、赤、青とすれば３番目の青と4番目の緑、6番目の青と7番目の緑が重なっています。青と緑が重なると、空色です。
すると上から順に上の穴を通った緑、上の穴を通った赤、上の穴を通った青＋真ん中の穴を通った緑＝空色、真ん中の穴を通った赤、真ん中の穴を通った青＋下の穴を通った緑＝空色、下の穴を通った赤、下の穴を通った青となるので、2番目は赤、7番目が青になります。
（答え）2番目　ア　7番目　イ

④　日光の下で赤く見えるものは、赤だけを反射します。したがって赤しか見えないので、3か所。
（答え）3か所

（４）①　赤と緑だけだと、青が入っているものとの区別ができないので、赤と赤紫、緑と空色が区別できません。
（答え）　ア、カ
②　
ア→ハチドリは人間が見えない光をとらえていますから、真っ暗がいっしょではありません。
イ→人間が見えない光をとらえているので、これも違います。
ウ→ハチドリが1色多いのですから、ハチドリのとらえる色の数の方が多くなります。
エ→人間に見えない色の模様があれば、ハチドリはその模様をとらえることができます。
（答え）エ

2022年第1回の問題です。

Ａ，Ｂ，Ｃ，Ｄの４人のうち１人だけ赤い帽子をかぶり，残りの３人は白い帽子をかぶっています。この４人が縦に１列に並んで次のような発言をしました。
　Ａ「私のすぐ後ろの人は赤色の帽子だ。」
　Ｂ「Ｄは私より前にいる。」
　Ｃ「私の帽子は白色だ。私より前の人は全員白色の帽子だ。」
　Ｄ「私のすぐ後ろの人は白色の帽子だ。」
この発言がすべて正しいとき，４人の並んでいる順を前から順に答えなさい。

【解説と解答】
条件を並べてみます。
Aのすぐうしろは赤→Aは赤ではない→Aは白
DはBより前
Cは白、Cより前は白
Dのうしろは白、
から赤はDかBです。
Bが赤だとすると、Bの前はA、Dは1番目か2番目で白、Cの前は白、だからCが2番目、Dが1番目となります。
D（白）C（白）A（白）B（赤）
Dが赤だとすると、Aの後ろがD、DのうしろがC（白）かB（白）
A（白）D（赤）B（白）C（白）にするとCの前が全員白にならないので×。
A（白）D（赤）C（白）B（白）でもCの前が全員白にならないので×。
したがって答えはD（白）C（白）A（白）B（赤）
（答え）DCAB

2022年洗足学園第3回の問題です

花子さんは３種類のノートＡ，Ｂ，Ｃを合計30冊買い，代金は6900円でした。１冊の値段はＡが300円，Ｂが240円，Ｃが165円です。ＡはＢの２倍より６冊少なく買ったとすると，Ｃは何冊買いましたか。ただし，価格はすべて税込みで考えます。なお，この問題は解答までの考え方を表す式や文章・図などを書きなさい。

という問題でした。

記述式なのですが、洗足の採点は「答えが間違っていた時に記述を見て部分点を決める」ということになっています。だからあまり詳しく書きすぎて時間をロスするのはもったいない。ここでは面積図などを書いてしまう方が簡単に解けて説明ができるかもしれません。

解答としてはつるかめ算を使ってしまうのが簡単で、以下のようになります。

AがBの2倍より６冊少ないので、300×６＝1800円加えると
6900＋1800＝8700円が全体になります。全部Cとすると６冊足したので全体が36冊になるから
165×36＝5940なので、差は8700―5940＝2760
AがBの2倍になっているので（300―165）×【2】＋（240―165）×【1】
＝【270】＋【75】＝【345】が2760円だから
2760÷345＝８
36―8×３＝12
（答え）12冊

これを面積図に書いてしまって、最後の部分の式だけを載せる、ぐらいで説明が済めば時間的にはそれほど時間がかからないでしょう。

2022年洗足学園第3回の問題です。

Ａ，Ｂの２つのコップがあり，Ａには食塩水，Ｂには水がそれぞれ400ｇずつ入っています。いまＡからＢに100ｇ移してよく混ぜてから，ＢからＡに100ｇ移したところ，Ａは濃度４％の食塩水になりました。最初にＡには何％の食塩水が入っていましたか。

【解説と解答】
Aに入っていた食塩を【4】とすると、100g移したのでBには【1】だけ行きます。
そのあとBからAに100g入れると全体が500gになっているので、BからAに100g入れると【0.2】食塩が戻ります。
Aの重さは400gで、濃度が4％だと食塩は16gでこれが【4】－【1】＋【0.2】＝【3.2】ですから【1】＝５g
したがってAに入っていた食塩は20gですから。20÷400×100＝５％
（答え）５％

2023年から洗足学園の入試は各回とも4教科になりました。

多くのお子さんが4教科で受験していることから、学校側としては2教科はもうなくしてもよいだろう、という判断になったのかもしれません。

が、実際にはやはり対策が大きく変わります。

洗足はこれまで第1回と第2回は、4教科受験生も含めて全員がまず算国2教科の判定を受けていたのです。

それでその合格枠に入れなかった子どもたちが、今度は4教科の判定を受けるということになったので、当然2教科で合格点が取れれば理科社会は見られない。

だから4教科の生徒であっても洗足の対策としては算数と国語２教科優先であったわけです。

しかし、来年はその制度がなくなるので、4教科で完全に勝負をしなければならない、ということになりました。そうなると、やはり特に大きな差を生むであろうと予想されるのが、理科です。

洗足の理科の出題は、化学、物理、生物、地学ときっちり大問４問で出題されますが、化学と物理はやはり計算問題が多いので、ここがしっかりできないといけない。

これまでまず２教科の選抜優先できたところでしたが、これからは理科計算をがんばらなければいけないので、少し受験層が変わる可能性があるかもしれません。

洗足学園は、2023年入試から第1回～第3回まですべて4教科で行うことになりました。

これまでは、第1回、第2回入試はまず算国2教科で採点して合格者を決めたのち、残りの定員について4教科で採点する形式がとられていましたが、ここのところ4教科受験生が多いこともあり、すべて4教科で行うことになりました。

算数、国語各50分　各100点
理科社会合わせて60分　各75点

したがって採点は基本的に全員4教科で行われることになるだろうと思われます。

詳しい募集要項は、学校ホームページに発表されますので、それまでお待ちください。

2022年第2回の出題。

図１の形をした容器に，水が深さ２cmまで入っています。この中に，底面の直径が２cm，厚さ１cmの円柱の形をしたコインを，図２のように４個ずつ積み上げた状態で全部で２００個を容器に並べます。水面の高さは何cmになりましたか。ただし，このコインは水にしずみます。

【解説と解答】
問題はコインが水面の上に来るか、全部水没するか、です。
水槽の底面積が21×17＝357
コインが占める底面積は200÷4＝50枚分ですから、
1×１×3.14×50＝157　したがって水が入る部分はちょうど200cm2になります。
水の体積は357×2＝714　714÷200＝3.57となり、4cmより小さいのでコインは全部水没していません。
（答え）3.57cm

6月7日、そごう横浜店9階の新都市ホールで、東京南部ならびにカナガワケンの女子高が一堂に会すイベントが行われます。

今年は完全予約、入場3部入れ替え制で、予約の開始は5月7日。

すでに22年目に入るイベントですが、洗足学園も参加します。女子校志望のみなさんには、良い機会となるでしょう。

詳しくは以下のホームページで
私触会

2022年　洗足学園　第2回の問題です。

長さが180ｍの電車Ａは時速60km で走ります。電車Ｂは，長さ600ⅿの橋をわたりきるのに２８秒かかります。電車ＡとＢが出会ってからすれちがうまでに９秒かかるとき，電車Ｂの長さは何ｍですか。なお，この問題は解答までの考え方を表す式や文章・図などを書きなさい。

【解説と解答】
電車Aの秒速は50/3mです。
電車Bの秒速を【1】mとすると、電車Bの長さ＋600＝【28】
一方電車AとBがすれ違う時には、電車Bの長さ＋180＝【9】＋50/3×9＝【9】＋150
したがって600－30＝【19】から電車Bの秒速は30ⅿ。
電車Bの長さは30×28－600＝240ｍ
（答え）240ⅿ

2022年洗足学園第1回の問題です。

下の図１は，正方形から４つの同じ形で大きさの等しい直角三角形を切り取ってつくった八角形です。この八角形の面積は265cm２で，８辺のうち４辺の長さは10cmでした。図２のように，八角形の10cmではない辺のそれぞれの真ん中の点を結んで四角形をつくったとき，この四角形の面積は何cm2ですか。

【解説と解答】

上図のように折り返したとき、八角形は★が８つと1辺が10cmの正方形になります。
したがって265－10×10＝165
165÷２＝82.5が★４つ分になるので、100＋82.5＝182.5

（答え）182.5cm2